pupSAT
GPU acceleration for SAT solving
Vikrant Gajria
Table of contents
Introduction
k-SAT solving is a well known NP-complete problem. A k-SAT formula is a boolean formula with $k$ literals in each clause. A formula is satisfiable if there exists an assignment to the variables such that the formula evaluates to true. The goal of a SAT solver is to find such an assignment. A SAT solver can be used to solve a variety of problems, such as scheduling, planning, and circuit design.
This project looks into code for popular serial SAT solvers like MiniSAT (http://minisat.se/) and MicroSAT to study the architecture of SAT solvers, and look for opportunities to parallelize the search process for GPU’s SIMD warps. The primary focus is on work done in expanding a node. Search-space optimizations such as work stealing are presented in other papers like HoardeSat and ManySat. The optimization here can be implemented into other parallel solvers, if implemented carefully to minimize memory moves between CPU and GPU.
The main algorithm for parallel unit propagation (pup) is shown in improv/main.cu.
An attempted solver is in src/purrsat.cu (incomplete). The practical algorithms that I’ve tried to implement are from this course: Practical SAT solving 2019, https://baldur.iti.kit.edu/sat/
Algorithms
DPLL algorithm
The most common algorithm for solving SAT is the Davis-Putnam-Logemann-Loveland (DPLL) algorithm. This algorithm is a recursive backtracking search. The algorithm works by assigning values to variables and then propagating the effects of these assignments. If the assignments lead to a contradiction, the algorithm backtracks and undoes the assignments. This algorithm is very inefficient in the worst case, but can be very fast in practice.
DPLL algorithm can be described with a flowchart below.
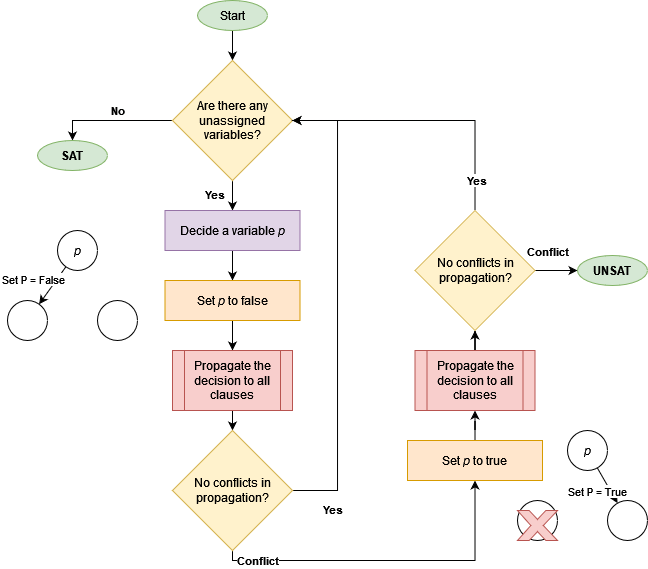
Bottleneck
The primary bottleneck in DPLL is unit propagation. According to zChaff’s creators, this step takes up 80-90% of the work done by SAT solvers. To speed-up this step, they came up with a lazy data-structure called 2-watched literals, which is an index with two pointers to every clause. As long as a clause has 2 un-assigned variables, the state of the clause is unknown.
This lazy index structure, in parallel SAT solvers, needs good concurrency control mechanisms. The approach to lock rows of the index is one way to enforce correctness, but this isn’t a good idea for SIMD warps of the GPU. The aim of a well-designed GPU kernel should be to limit warp divergence, and make sure that every thread in a warp does almost the same amount of work. By this idea, we can let go of some lazy aspects of the index and thus
Approach to solving bottleneck
Unit propagation loop
A basic unit propagation loop is explained below:
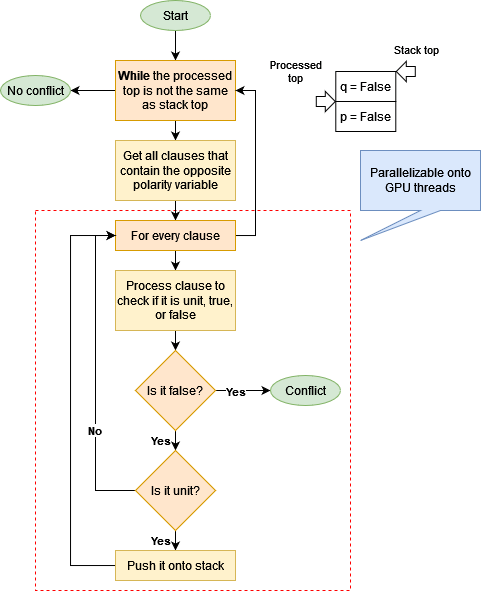
Observe that the task of analyzing every clause does not depend on any other clause’s analysis. A separate thread can anlyze a set of clauses and come up with its local assignment, which then can be combined with local assignments of other threads and checked in the end for conflicting assignments. An assignment is said to have a conflict if a variable $v$ appears as both postive $v$ and negative $\not v$ in the assignment.
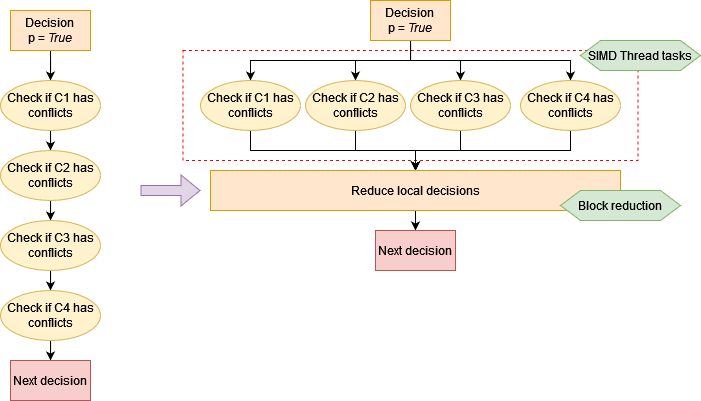
Parallel algorithm
Implementation
Assumptions
The algorithm above is implemented assuming that the input formula matrix and variable index will remain unchanged during the execution of the algorithm.
GPU-CPU data structures
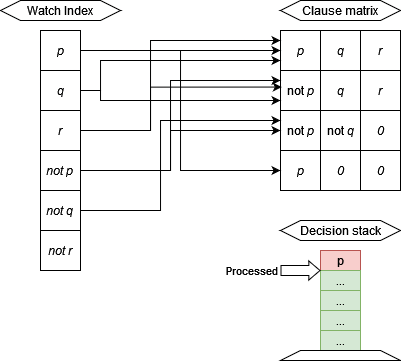
For a k-SAT problem with $c$ clauses and $v$ variables, each clause containing a maximum of $k$ variables. Data structures are designed to be managed between both host and device, where the device tries to avoid modifying the data structures as much as possible to reduce memory I/O.
Formula matrix
The formula matrix is a $c \times k$ 2D matrix that contains variables numbered $1 \dots v$. The variables are in the range $[-v, v]$. A $0$ variable indicates a gap in the clause (such as a clause with less than $k$ variables in it). Typically, $k « v$, such as $k = 3$ for 3-SAT while $v$ could be more than 512. Due to the small size of $k$, the formula can be loaded into shared memory with coaelsced reads of GPU for faster processing.
Refer: struct Formula in improv/main.cu:56
Index structure
The index structure is a $2v \times c + 2v$ 2D matrix that indexes the occurences of positive and negative literals of variables in clauses $l \rightarrow c$. Additional cell is used in each literal row to indicate the number of occurences. A sparse representation can also be created for this and the previous matrix.
Refer: struct Index in improv/main.cu:20
Decisions trail
A decision trail is a stack of assignment decisions made for state space search. This structure contains a size of maximum size $v$ and a hash-set of size $v$ to maintain whether a variable is present in the trail or not. This allows for $O(1)$ checking of variable assignment and $O(1)$ deciding or backtracking (down and up the state space tree). Optimization for this structure include bitvector representations for assignments as done in previous semester.
Refer: struct Decisions in improv/main.cu:79
Parallel work
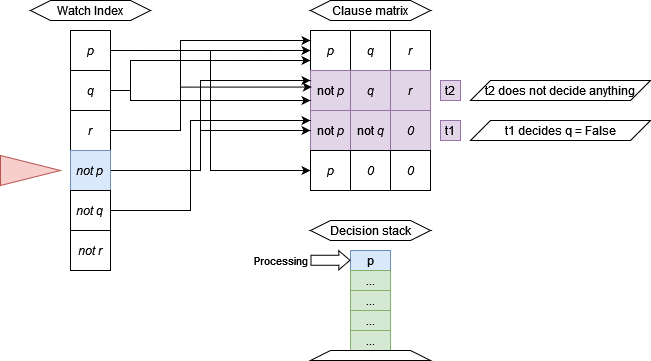
Unlike my previous semester’s work where I placed $c$ threads on every row of the matrix, in this semester’s work, I focussed more on reducing the number of threads required to operate on decisions by using an index structured inspired by zChaff SAT solver. This allows for a reduced number of processors $p$ and thus a lower parallel cost.
For every unprocessed decision, threads access the list of clauses that contain the opposite literal. That is, if the solver decides $p = True$, then the threads access the list of clauses where $\not p$ occurs. The threads then process the clause to check if it has no unassigned variables (the clause cannot be satisfied) or whether the clause has only one unassigned variable (the clause is now a unit clause). If a clause is unsatisfied, the kernel returns with an error status.
Reduction of partial assignments
Once the local unit clauses are calculated, each thread has zero or one decision (that is, each thread can choose to produce a decision). These decisions are placed into a shared memory array. A chosen thread serially pushes the decisions onto the stack. If a conflicting decision was already present on the stack, then the unit propagation procedure returns with conflict status.
Optimization: Parallel push to the stack with coalesced writes
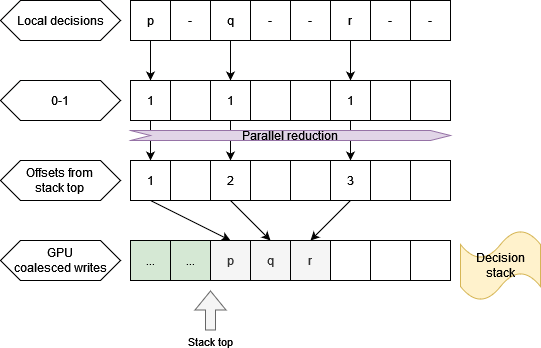
An optimized approach is to assign locations for every thread to place their local decisions onto the stack. The stack is implemented with an array. The threads decide cumulative positions to place their data and write to the stack in coaslesced fashion. If a thread is assigned a location that is beyond the size of the decisions stack (size: $V$), then it follows that there must exist a conflicting decision on the stack. This is because we cannot decide values for more than $V$ variables.
Number of threads
The kernel dispatch dimensions will depend on the distribution of variables in clauses. That is, there is no optimal block size for every SAT instance or category of problem (graph coloring, uniform random 3-SAT…). However, it’s best to keep the block size in multiples of 32 as with any other CUDA kernel.
Number of blocks
Currently this algorithm only works with 1 block.
Heuristics, learning-driven search, massively parallel solvers
This work is intended to be added to other massively parallel SAT solvers that parallelize state space search. Examples of such solvers include ManySAT and HoardeSAT that generate several random assignments and task workers to explore the state space search, they incorporate strategies such as work-stealing and clause sharing. There are some very simple parallel solvers that perform great, such as PPfolio solver that is described as “it’s probably the laziest and most stupid solver ever written, which does not even parse the CNF and knows nothing about the clauses”. Simple ideas work pretty well in SAT solvers. See: https://www.cril.univ-artois.fr/~roussel/ppfolio/
Non-chronological back-tracking and conflict learning
Conflict-Driven Clause Learning (CDCL) is a modification to DPLL, wherein the algorithm backtracks multiple levels up the search tree and adds new clauses to learn from its previous mistakes. The base algorithm is pretty much the same, in that it still uses unit propagation. This project’s algorithm can be implemented in CDCL solvers as well to take advantage of heuristics and non-chronological backtracking. I found it a difficult to implement in that there’s a lot of memory copies between host and device, therefore it wasn’t possible for me to think of a good way to minimize memory transfers.
Implementing an implication graph
Implication graph for CDCL is a graph that is used for learning from mistakes. It is a acyclic directed graph. It can be implemented using the DecisionStack structure mentioned in this project.